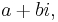Order (ring theory)

In mathematics, an order in the sense of ring theory is a subring $\mathcal{O}$ of a ring $R$ that satisfies the conditions

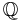
R is a ring which is a finite-dimensional algebra over the rational number field $\mathbb{Q}$
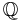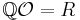$\mathcal{O}$ spans R over $\mathbb{Q}$ , so that $\mathbb{Q} \mathcal{O} = R$ , and
$\mathcal{O}$ is a lattice in R.

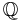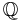The third condition can be stated more accurately, in terms of the extension of scalars of R to the real numbers, embedding R in a real vector space (equivalently, taking the tensor product over $\mathbb{Q}$ ). In less formal terms, additively $\mathcal{O}$ should be a free abelian group generated by a basis for R over $\mathbb{Q}$ .

The leading example is the case where R is a number field K and $\mathcal{O}$ is its ring of integers. In algebraic number theory there are examples for any K other than the rational field of proper subrings of the ring of integers that are also orders. For example in the Gaussian integers we can take the subring of the

$a%2Bbi,$

for which b is an even number. A basic result on orders states that the ring of integers in K is the unique maximal order: all other orders in K are contained in it.

When R is not a commutative ring, the idea of order is still important, but the phenomena are different. For example, the Hurwitz quaternions are a maximal order in the quaternions with rational co-ordinates; they are not the quaternions with integer coordinates in the most obvious sense. Maximal orders exist in general, but need not be maximum orders: there is in general no largest order, but a number of maximal orders. An important class of examples is that of integral group rings.

Because there is a local-global principle for lattices the maximal order question can be examined at a local field level. This technique is applied in algebraic number theory and modular representation theory.

Definition

An order $R$ in a number field $K$ is a subring of $K$ which as a $\mathbb{Z}$ -module is finitely generated and of maximal rank 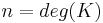$n=deg(K)$ (note that we use the "modern" definition of a ring, which includes the existence of the multiplicative identity 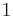$1$ ).^[1]

References

^ Henri Cohen, A Course in Computational Algebraic Number Theory 3rd corrected printing, pp. 181, 1996, Springer

Order (ring theory)

Definition

References

See also